next up previous contents
Next: Layered Examples Up: Examples and Results Previous: Two Simple Examples   Contents

Self-contained Examples

The score for audio example 8 is printed in Table 5.6.

Table 5.6: The score for audio example 8.
\begin{table}\frame{\begin{minipage}{6in} {\singlespace \verbatiminput{audio/bark/bark.sc}} \end{minipage}} \end{table}


The time segmentation in this example is 20 to 1, and the different partials are added to the sound from top to bottom. The spectrogram of the whole duration and three seconds of the sound, which is 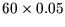$60 \times 0.05$, is illustrated in figure 5-35.4.

Figure 5-3: The spectrogram of the first 60 and the first 3 seconds of audio example 8 is illustrated. The spectrogram of the first 3 seconds is rescaled by a factor of 0.4. As it can be seen, the same structure is manifested in this sound in two levels of our auditory perception.
\begin{figure}\epsffile{audio/bark/newsound.ps}\epsffile{audio/bark/newsound.3.ps}\end{figure}

As it can be seen, the same structure is manifested in both spectrogram. Almost any picked segment according to the similarity factors of this sound manifests the same structure. For example the segments 3.0-5.85 ( $5.85 = 3 + 3 \times 0.95$) is a scaled down version of the segment 0.0-3.0. This similarity can be seen as an exponentially decaying shape in the lower spectrum of the sound. The sound starts with this shape and at the same time that the listener is becoming aware of this decaying shape, the larger picture of the sound emerges, which is the similarity of the ending segments 0-60, 3-60, 5.85-60, etc.

The time segmentations of 0.05 to 0.95, or frequency factors of 0.4 and 0.9, may look arbitrary. In fact, in the process of the development of the system, the examples which we have called self-contained started as experimentations and the numbers were tuned with every listening. In this paradigm, one is able to work with smaller versions of the sound for development and tuning, and in this way save time in the synthesis process. Table 5.7 is the score for audio example 9, which is a short version of the previous example.

Table 5.7: The score for audio example 9.
\begin{table}\frame{\begin{minipage}{6in} {\singlespace \verbatiminput{audio/bark/short.sc}} \end{minipage}} \end{table}


All the frequency partials in the previous examples were geometrically related to each other. We can create harmonically related partials by using expressions for frequency factors. The score for the audio example 10 is printed in table 5.8 and figure 5-4 illustrates the spectrogram for this audio example.

Table 5.8: The score for audio example 10.
\begin{table}\frame{\begin{minipage}{6in} {\singlespace \verbatiminput{audio/water/water.sc}} \end{minipage}} \end{table}


Figure 5-4: The spectrogram of audio example 10 is illustrated.
\begin{figure}\epsffile{audio/water/newwater.ps}\end{figure}

next up previous contents
Next: Layered Examples Up: Examples and Results Previous: Two Simple Examples   Contents
Shahrokh Yadegari 2001-03-01