Conclusions

This section has tried to touch upon a few different issues concerning $1/f$ noise. In general we view signals as either random or deterministic. If a signal is not periodic and has an infinite amount of energy and all its maximum and minimum values are in a finite range, with our present state of signal processing we must treat the signal as random. However, if the signal has finite energy (and a finite number of discontinuities) we will be able to mathematically, rather than statistically, derive and specifically apply the Fourier transform theorem (Dirichlet conditions[48, page 84]) to the signal. A $1/f$ signal lives on the border of these dichotomy. 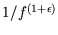The high frequency energy of a $1/ {f}^{(1 + \epsilon)}$ spectrum is finite, while the high frequency region of a $1/f$ spectrum is infinite. The power spectrum of random processes is usually also divided into two sections, a high frequency region with a slope steeper than $1/f$ and close to $1 / {f}^{2}$, and the low frequency region which is flat. The flat low frequency region implies that there is no long-term correlation in the signal, while the steep high frequency slope implies a short-term correlation. Keshner[20] points out:

The presence of $1/f$ noise in MOSFET's, down to the lowest frequency allowed by the limited observation time, suggests that the division into just two subsystems is inappropriate.

The $1/f$ noise is an evolutionary signal, meaning that its whole past history effects is present and future state. This implies a certain type of memory in a $1/f$ process. Dodge[9] finds fractals and noise to be an interesting paradigm for computer-aided composition. He also suggests that the ``memory'' of noise can account for its success.

The study of music as a $1/f$ noise has a certain value, in that it treats a musical signal as a physical signal. The uniformity that a $1/f$ model of music suggests exists on all levels of our perception down to about 5 Hz. There are no psychological issues to be considered. This is not to undermine the psychological implication of music, but rather to suggest that if we would like to make comments about music in a scientifically rigorous paradigm, it is possible, as we really should, to ignore all psychological issues (the most important of all of them being the assumption of ``intelligence''). The study of music as $1/f$ noise assumes no intelligent entity except the music itself.