



Next: Conclusions
Up: The Ubiquitous Noise
Previous: in Music
Contents
In this section we will present the result of our analysis of the pieces
we had access to.
Rather than looking at the audio signal, we took a different
route for our analysis. We used the data from 57 pieces which were coded
in MIDI file format. We extracted a top voice from these pieces.
The top voice is defined as the highest sounding pitch at any moment.
Silences were eliminated by extending the last highest pitch. The
data was stored as described in section 4.4.1.
The tempo was set by the first tempo marking and all other tempo changes
during the piece were ignored.
The DC value of the pitch signal was subtracted from all samples
and the power spectrum of the resulting signal was computed.
We would like to emphasize the fact that we are not saying that such a
signal is ``the'' melody of the piece; however, we are assuming that with the
defined procedure we will obtain ``a'' melody which has some musical
integrity.
Audio example 3 is the resynthesis of the first 30 seconds of the
pitch signal extracted from the J. S. Bach's 3rd Brandenburg concerto.
As it can be clearly heard, there are still problems in the extraction
method which, due to not having enough time, we did not solve.
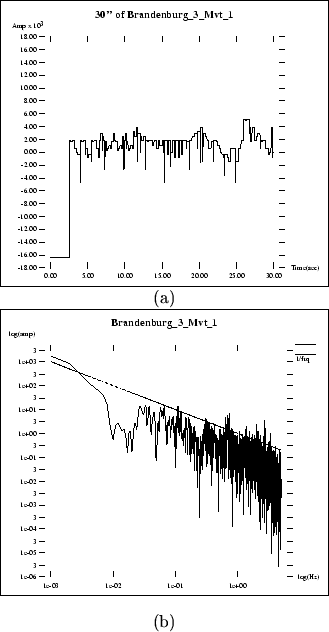
Figure 4-7 shows the first 30 seconds of the extracted
pitch signal and the power spectrum computed for the
duration of piece. The problems of the extraction method can be seen as the
vertical spikes in the figure. As it can be seen, the power spectrum of this
signal is best fitted by the  line. Appendix A
contains the result of all the pieces whose power spectrum were
systematically computed.
line. Appendix A
contains the result of all the pieces whose power spectrum were
systematically computed.
Figure 4-7:
(a) is the first 30 seconds of the ``top voice'' signal
extracted from J. S. Bach's 3rd Brandenburg Concerto. (b) is the the power
spectrum of the ``top voice'' signal for the duration of the piece. Notice
that the line representing the  line fits the slope of the power
spectrum.
line fits the slope of the power
spectrum.
 |
Almost all pieces behaved very closely to the  noise.
It is worth noting that we were able to find the fault of our extraction
method by looking at the resulting power spectrums, and that shows
that the power spectrum does carry useful analysis information.
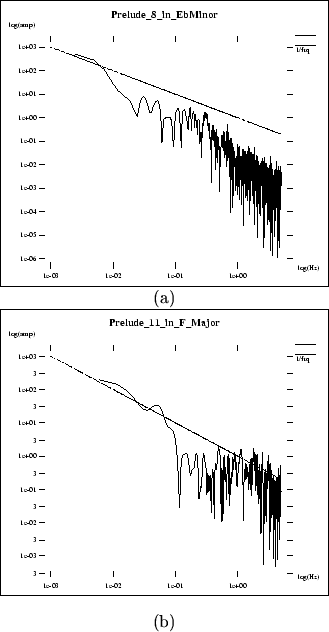
For example, the power spectrum of Prelude 11 from the first book of the
Well-tempered Clavier (see figure 4-8-b) was the most odd
looking
spectrum. When we listened to the extracted signal we found that the
many trills of the dotted quarters (which are scattered throughout the piece)
mixed with the bottom voice created a ``noisy'' melody which accounts for the
flat section of the spectrum between .1 to 5 Hz. The slope of the power
spectrum is a good measure of how much material is coded in the melody.
For example, the spectrum of Prelude 8 (see figure 4-8-a)
showed a slope steeper than other
pieces, which should mean that the melody of the extracted signal should
be more correlated than the others.
When we looked at the score for that piece, we noticed that
much of the melody is coded in other voices rather than the top voice,
and the highest pitch is kept for long periods of time; in one case
(measures 32 to 34) the highest note is kept sounding for 3 full measures.
noise.
It is worth noting that we were able to find the fault of our extraction
method by looking at the resulting power spectrums, and that shows
that the power spectrum does carry useful analysis information.
For example, the power spectrum of Prelude 11 from the first book of the
Well-tempered Clavier (see figure 4-8-b) was the most odd
looking
spectrum. When we listened to the extracted signal we found that the
many trills of the dotted quarters (which are scattered throughout the piece)
mixed with the bottom voice created a ``noisy'' melody which accounts for the
flat section of the spectrum between .1 to 5 Hz. The slope of the power
spectrum is a good measure of how much material is coded in the melody.
For example, the spectrum of Prelude 8 (see figure 4-8-a)
showed a slope steeper than other
pieces, which should mean that the melody of the extracted signal should
be more correlated than the others.
When we looked at the score for that piece, we noticed that
much of the melody is coded in other voices rather than the top voice,
and the highest pitch is kept for long periods of time; in one case
(measures 32 to 34) the highest note is kept sounding for 3 full measures.
Figure 4-8:
The spectrum of two of the odd cases of the analysis is shown.
Figure (a) is the power spectrum of the ``top voice'' signal of the 8th prelude
from J. S. Bach's Well-tempered Clavier Part I. Notice that the slope of the
spectrum is sharper than the  line and that can be explained by the
static melody of the top voice in that piece. Figure (b) is the power spectrum
of the 11th prelude from J. S. Bach's Well-tempered Clavier Part I. Notice
that the spectrum is flat in the 0.1-5 Hz region. This effect was caused
by the way we extracted the top voice. The interaction between
the half note trills and our down-sampling of the MIDI data
created a noisy melody which
is characterized by a flat spectrum.
line and that can be explained by the
static melody of the top voice in that piece. Figure (b) is the power spectrum
of the 11th prelude from J. S. Bach's Well-tempered Clavier Part I. Notice
that the spectrum is flat in the 0.1-5 Hz region. This effect was caused
by the way we extracted the top voice. The interaction between
the half note trills and our down-sampling of the MIDI data
created a noisy melody which
is characterized by a flat spectrum.
 |




Next: Conclusions
Up: The Ubiquitous Noise
Previous: in Music
Contents
Shahrokh Yadegari
2001-03-01


![]() noise.
It is worth noting that we were able to find the fault of our extraction
method by looking at the resulting power spectrums, and that shows
that the power spectrum does carry useful analysis information.
For example, the power spectrum of Prelude 11 from the first book of the
Well-tempered Clavier (see figure 4-8-b) was the most odd
looking
spectrum. When we listened to the extracted signal we found that the
many trills of the dotted quarters (which are scattered throughout the piece)
mixed with the bottom voice created a ``noisy'' melody which accounts for the
flat section of the spectrum between .1 to 5 Hz. The slope of the power
spectrum is a good measure of how much material is coded in the melody.
For example, the spectrum of Prelude 8 (see figure 4-8-a)
showed a slope steeper than other
pieces, which should mean that the melody of the extracted signal should
be more correlated than the others.
When we looked at the score for that piece, we noticed that
much of the melody is coded in other voices rather than the top voice,
and the highest pitch is kept for long periods of time; in one case
(measures 32 to 34) the highest note is kept sounding for 3 full measures.
noise.
It is worth noting that we were able to find the fault of our extraction
method by looking at the resulting power spectrums, and that shows
that the power spectrum does carry useful analysis information.
For example, the power spectrum of Prelude 11 from the first book of the
Well-tempered Clavier (see figure 4-8-b) was the most odd
looking
spectrum. When we listened to the extracted signal we found that the
many trills of the dotted quarters (which are scattered throughout the piece)
mixed with the bottom voice created a ``noisy'' melody which accounts for the
flat section of the spectrum between .1 to 5 Hz. The slope of the power
spectrum is a good measure of how much material is coded in the melody.
For example, the spectrum of Prelude 8 (see figure 4-8-a)
showed a slope steeper than other
pieces, which should mean that the melody of the extracted signal should
be more correlated than the others.
When we looked at the score for that piece, we noticed that
much of the melody is coded in other voices rather than the top voice,
and the highest pitch is kept for long periods of time; in one case
(measures 32 to 34) the highest note is kept sounding for 3 full measures.
