Self-similarity of $1/f$ Noise

The scale invariancy of the signal can be explained by the simple scaling rule of Fourier transforms.

$$S_{f}(f) = 1/f$$ (4.9)

$${\cal R}_f(\tau) = {\cal F}^{-1}(S_{f}(f)) = \ {\cal F}^{-1}(1 / f)$$ (4.10)

$${\cal R}_f(\alpha \tau) = {\cal F}^{-1}(\frac{1}{\alpha} {S_{f}}(f /\alpha))$$

$$= {\cal F}^{-1}(\frac{1}{\alpha} \times \ \frac{\alpha}{f })$$

$$= {\cal F}^{-1}(1 / f)$$ (4.11)

From equations 4.10 and 4.11 we can conclude:

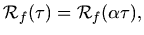$${\cal R}_f(\tau) = {\cal R}_f(\alpha \tau),$$ (4.12)

which means that our auto-correlation function is scale independent, or in the other words the auto-correlation function is a fractal. We should note that most observed $1/f$ signals are random signals. Mandelbrot[28] suggests that these signals should be treated as nonstationary random signals to get around the infinite invariance problems. Thus, the autocorrelation and spectrum of $1/f$ noise would be time-dependent. The problem with infinite invariance is that a true self-similar signal has an infinite amount of energy in its high spectral region. In the case of the $1/f$ signal the integral:

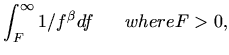$$\int_{F}^{\infty} 1/{f}^{\beta} df \ \ \ \ \ where F > 0,$$ (4.13)

is finite when $\beta > 1$, and infinite when $\beta < 1$. This border is where we make the distinction between random and deterministic signals. Notice that the equation 4.12 holds for any 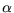$\alpha$, and that fact should be interpreted as the statistical behavior of the signal. There is no one-to-one relationship between a power spectrum and a signal. Many different signals in time may have the same power spectrum. If we were dealing with a deterministic signal and not a random process, one way we could explain equation 4.12 is that the auto-correlation function has to be a DC function. However, the fluctuations of the observed phenomena which exhibit a $1/f$ power spectrum are far more erratic than unit functions. (For rigorous mathematical treatment of $1/f$ noise see Keshner[20], Flandrin[12], Wornell[51].)