What is Chaos?

Until recently signals were categorized as either being deterministic or random. If a deterministic signal was an oscillating signal and had an infinite amount of energy it was supposed to be periodic. The discovery of chaotic systems meant that this assumption no longer holds. When Lorenz detected chaos, he called it: ``Deterministic Nonperiodic Flow''[26]. Chaos was an observed phenomenon which went against the usual scientific intuition; obviously intuition is a highly subjective matter and one should create ones own perception of this statement. Lorenz studied the phenomenon of convection in fluids. 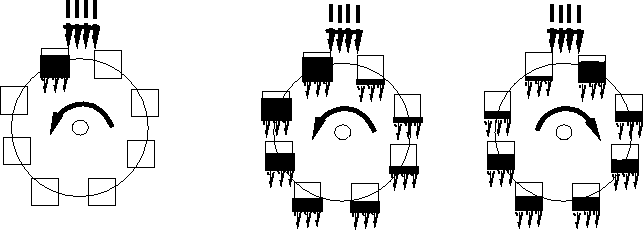However, his equations can be mapped to a very simple mechanical system. Imagine a water-wheel with many buckets connected to it (see Figure 3-3). All the buckets have holes in the bottom so that the water can run out. A steady flow of water is supplied from the top. If the wheel is started with a small push, the buckets on the top are filled and by the time they reach the bottom, they are mostly empty. Therefore, one side of the wheel becomes heavier than the other. If we increase the flow of the water the wheel starts to turn faster. Once we have passed a certain threshold, the system can start to act chaotic. The wheel can turn so fast that by the buckets which reach the bottom of the wheel are not completely empty, and the buckets that pass under the flow do not have enough time to fill up, and the wheel starts to get slower, then it gets slow enough that the original situation causes it to speed up again. This oscillation becomes damped to the point that the wheel starts to turn the other way around; this means that the oscillation of getting faster and slower damps out at the point that if the wheel was turning to the right, the left buckets would be heavier and the wheel starts to turn in the other direction. What would happen if we let such a system ``cool down'' without changing any parameters? This is where the scientific intuition used to provide different answers than nature. One may think that the system will eventually pick up a pattern, however long this pattern may be, and keep repeating that pattern. Lorenz showed that this system will never repeat itself, which means that even though the behavior of the system is called deterministic (i.e., three differential equations model the system), the resulting behavior is nonperiodic. Lorenz explained such behavior by showing that the phase-space of this system contains a space which is created from volumeless surfaces with infinitely detailed structure.

Figure 3-3: Water-wheel imitating the convection system of Lorenz[14].