Recreated Results

One could argue that if we start with 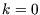, we are actually creating partials which are lower than the audibility range (less than 20 Hz). And by rescaling the signal (playing it faster) we are only changing the audible high frequency spectrum. For that reason we start the partials from 32 Hz. Audio example 1 is an example of a Weierstrass function with and , therefore, the sound is composed of geometrically related partials from 32 to 4096. The example was created ^4.1at a sampling rate of 22050 Hz. It is first played at a sampling rate of (22050 Hz) and then at double that rate (44100 Hz). Even though one notices that the center of mass of the energy has increased in the frequency spectrum, one does not get the feeling that the pitch has moved one octave higher. The self-similarity of this signal can be seen in figure 4-1. In figure 4-1-a the first 346 samples (which at a sampling rate of 22050 Hz is about 16 milliseconds), is plotted against exactly half () of those samples in figure 4-1-b.

Figure 4-1: A simple Weierstrass function with and $k = 5,6,...,12$. (a) shows the starting 346 samples at sampling rate of 22050 Hz and (b) shows exactly half of that signal (the starting 173 samples). Notice that the two shapes differ only in high frequency details. This similarity can be seen in higher or lower time scales as well.

Figure 4-2: A Weierstrass function with $\beta = 2.1189$ and $k = 5,6,...,12$. (a) and (b) are the first 205 and 97 ( $205 / 2.1189$ ) samples.

By carefully choosing $\beta$, we can create a signal whose perceived pitch will descend by a semitone when the signal is played at twice the speed. Therefore the relationship between the new $\beta$ and scaling value (which is 2 since we are playing at twice the sampling rate), should be the twelfth root of two (the frequency multiplier for a semitone). Therefore:

$$\beta = 2 \sqrt[12]{2} \simeq 2.1189$$ (4.4)

Audio example 2 is an example of a Weierstrass function with and . Again, the sound is played at the original sampling rate (22050 Hz) and then played at twice the sampling rate (44100 Hz). The self-similarity of this signal in the time domain can be seen in figure 4-2. Listen to this and the previous example at first with no attempt to find the pitch, and you will simply hear the movement of the mass of frequencies. Then, listen to the examples while concentrating on finding a pitch, and notice that the paradox effects gets stronger.