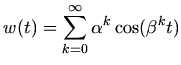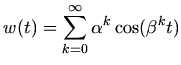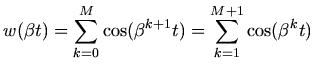Next: Recreated Results
Up: Self-similarity in Sound and
Previous: Introduction
Contents
The Shepard Tone
The partials of harmonic sounds are related to each other by
an arithmetical relationship.
The partials of a Shepard Tone are related to
each other by a geometrical relationship. Shepard
used such signals to prove his hypothesis of the circularity of
pitch perception[45].
Schroeder[43, page 96] shows that the auditory paradox
created by the
Shepard Tone, which is generated according to a Weierstrass function,
has become possible due to the self-similarity
of the signal. A Weierstrass function is constructed as follows:
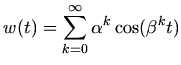 |
|
|
(4.1) |
where 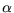 is real and
is real and  is odd. Weierstrass showed that under
certain conditions of
is odd. Weierstrass showed that under
certain conditions of 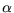 and
and  ,
this function is everywhere continuous
but nowhere differentiable. For creating a Shepard tone we can drop
the
,
this function is everywhere continuous
but nowhere differentiable. For creating a Shepard tone we can drop
the  term since we are only going to be dealing with
a finite number of partials. Therefore, we have:
term since we are only going to be dealing with
a finite number of partials. Therefore, we have:
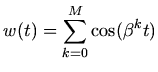 |
|
|
(4.2) |
where  is the number of partials and
is the number of partials and  is the geometrical
relationship between two adjacent partials.
Although Shepard applies a formant-like envelope to the
frequency domain representation of the signal, this is done for smoothing
the perceptual transition and sustaining the paradox effect. The paradox
is created from the fact that the ear attempts to extract a
one-dimensional signal
(the variable being pitch) out of a multidimensional signal (timbre).
We can think of pitch as a value which identifies a relationship between
the partials of a signal in a one-dimensional way.
If we view the frequency domain representation of the signal, then time scaling
according to the same geometrical relationship
is the geometrical
relationship between two adjacent partials.
Although Shepard applies a formant-like envelope to the
frequency domain representation of the signal, this is done for smoothing
the perceptual transition and sustaining the paradox effect. The paradox
is created from the fact that the ear attempts to extract a
one-dimensional signal
(the variable being pitch) out of a multidimensional signal (timbre).
We can think of pitch as a value which identifies a relationship between
the partials of a signal in a one-dimensional way.
If we view the frequency domain representation of the signal, then time scaling
according to the same geometrical relationship  does not change
the ``body''
of the signal but only its boundary conditions; therefore we hear the same
pitch and not a pitch scaled according to the scale factor.
Scaling the function
does not change
the ``body''
of the signal but only its boundary conditions; therefore we hear the same
pitch and not a pitch scaled according to the scale factor.
Scaling the function  in time by a factor of
in time by a factor of  gives
gives
 : substituting into equation 4.2, we get:
: substituting into equation 4.2, we get:
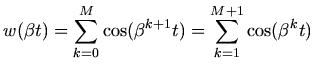 |
|
|
(4.3) |
which is the same as  except for the boundary conditions of
except for the boundary conditions of 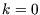 and
and  .
.
Subsections




Next: Recreated Results
Up: Self-similarity in Sound and
Previous: Introduction
Contents
Shahrokh Yadegari
2001-03-01