



Next: List of Tables
Up: Self-similar Synthesis: On the
Previous: Contents
Contents
- Square Limit by M. C. Escher
- Square Limit progression
- Water-wheel imitating the convection system of
Lorenz[14].
- The Koch Snowflake
- The asymptotically self-similar Hilbert curve. Notice the effect
of aliasing when the details exceed the resolution of
the printer or screen.
- A simple Weierstrass function with
 and
and
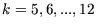 .
(a) shows the starting 346 samples at sampling rate of 22050 Hz and
(b) shows exactly half of that
signal (the starting 173 samples). Notice that the two shapes differ only
in high frequency details. This similarity can be seen in higher
or lower time scales as well.
.
(a) shows the starting 346 samples at sampling rate of 22050 Hz and
(b) shows exactly half of that
signal (the starting 173 samples). Notice that the two shapes differ only
in high frequency details. This similarity can be seen in higher
or lower time scales as well.
- A Weierstrass function with
 and
and
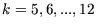 .
(a) and (b) are the first 205 and 97 (
.
(a) and (b) are the first 205 and 97 ( 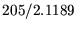 ) samples.
) samples.
- The time domain and power spectrum of white noise with average
duration of 0.1 seconds. (a) illustrates the first 30 seconds of the signal
and (b) is the power spectrum of such a signal in log-log scale.
The line representing the
 is also drawn for reference. Notice that
the power spectrum for this signal is flat for the area of our inspection
which is between 0.001 and 5 Hz.
is also drawn for reference. Notice that
the power spectrum for this signal is flat for the area of our inspection
which is between 0.001 and 5 Hz.
- The time domain and (log-log scale) power spectrum of random signals
with average duration of 0.5, 2, and 200 are illustrated.
The line representing the
 line is also drawn for reference.
Notice that the power spectrums show a slope steeper than the
line is also drawn for reference.
Notice that the power spectrums show a slope steeper than the  line
in the area of correlation while the rest of the spectrum stays flat.
line
in the area of correlation while the rest of the spectrum stays flat.
- In this figure the effect of bad quantization of a random signal
is illustrated. The values of a random signal are truncated to the quantized
level rather than being rounded to the nearest level. This figures should be
compared to the first illustration of figure 4-4.
Notice how the low frequency power increases as we use fewer quantization
levels.
- The first 30 seconds and the power spectrum of a random signal with
a simple deterministic shape added to it is illustrated. The deterministic
shaped is scaled to the duration of the note. Notice that such a process
shows up as low frequency (i.e. long term correlation) on the power
spectrum.
- (a) is the first 30 seconds of the ``top voice'' signal
extracted from J. S. Bach's 3rd Brandenburg Concerto. (b) is the the power
spectrum of the ``top voice'' signal for the duration of the piece. Notice
that the line representing the
 line fits the slope of the power
spectrum.
line fits the slope of the power
spectrum.
- The spectrum of two of the odd cases of the analysis is shown.
Figure (a) is the power spectrum of the ``top voice'' signal of the 8th prelude
from J. S. Bach's Well-tempered Clavier Part I. Notice that the slope of the
spectrum is sharper than the
 line and that can be explained by the
static melody of the top voice in that piece. Figure (b) is the power spectrum
of the 11th prelude from J. S. Bach's Well-tempered Clavier Part I. Notice
that the spectrum is flat in the 0.1-5 Hz region. This effect was caused
by the way we extracted the top voice. The interaction between
the half note trills and our down-sampling of the MIDI data
created a noisy melody which
is characterized by a flat spectrum.
line and that can be explained by the
static melody of the top voice in that piece. Figure (b) is the power spectrum
of the 11th prelude from J. S. Bach's Well-tempered Clavier Part I. Notice
that the spectrum is flat in the 0.1-5 Hz region. This effect was caused
by the way we extracted the top voice. The interaction between
the half note trills and our down-sampling of the MIDI data
created a noisy melody which
is characterized by a flat spectrum.
- The frequency fluctuation of the audio example 4 is
illustrated. (a) shows the frequency fluctuation in 2 seconds and (b) shows
the frequency fluctuation in 1 second. The basic shape of
both graphs are similar to each other.
- The frequency fluctuation of the audio example 5 is
illustrated. (a) shows the frequency fluctuation in 2 seconds and (b) shows
the frequency fluctuation in 0.667 second. The basic shape of
both graphs is a triangle.
- The spectrogram of the first 60 and the first 3 seconds of audio
example 8 is illustrated. The spectrogram of the first 3 seconds
is rescaled by a factor of 0.4. As it can be seen, the same structure
is manifested in this sound in two levels of our auditory perception.
- The spectrogram of audio example 10 is illustrated.
- The spectrogram of sound example 11 is illustrated.
- The time segmentation of the first 4 levels for audio
example 15 is illustrated. This example has a two-level hierarchy.
The first level goes through a binary segmentation, and the first part of
the second level goes through a trinary segmentation. The time segments
which have gone through a trinary segmentation are shaded.
Shahrokh Yadegari
2001-03-01